Главная › Блоги › Блог GogA

Мини-конкурс №4: любимая геометрия (1 грамм золота)

Опубликовано GogA в Вс, 23/11/2008 - 07:07

Да-да, я любил в школе геометрию. Конечно не так сильно как информатику, но любил. Сегодня (лукавлю), нашёл и решил одну геометрическую задачку (пару месяцев назад не смог решить). Задачка мне понравилась, поэтому решил предложить решить её Вам.

Ну а чтобы немного подогреть Ваш интерес, решил сделать небольшой приз, а именно 1 грамм Золота ;)

Задачка под катом :)

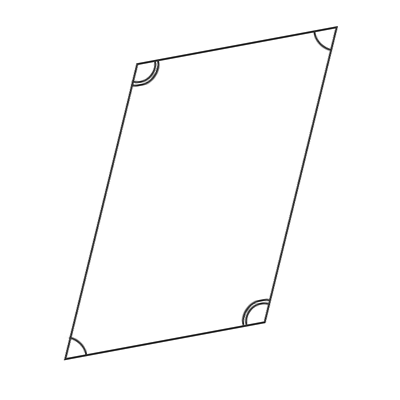
Как разделить фигуру ниже на девять равнобедренных треугольников? (Дан четырёхугольник, у которого равны между собой противоположные углы).

Задачку решил не выкладывать в рабочее время, а то в прошлый раз y некоторых отобрал ценное рабочее время (аж несколько часов). Да, и в Мини-конкурсе № 3: опять монтажник было два победителя, а не один, как предполагалось :) Участники nepod и amastercar почти одновременно прислали правильный ответ (разница две минуты). Учитывая то что Nepod два часа высчитывал, сколько будет путь монтажника (имея верный план маршрута), ответ от amastercar я заметил несколько позже. Но всё равно каждый получил по призу.

Учитывая что доллар не подкреплён золотом (а вы не знали? Смотрите: раз и два, даже если знали — посмотрите), а золото является одним из лучших вариантов инвестиций сейчас, приз будет в жёлтом металле. И будет выплачен первому приславшему верный ответ на мою почту в эквиваленте WMG (WebMoney Gold). А стоит нынче золото ~$800 за тройскую унцию.

Интересно? Жду ответы на почту sasha@gogolev.net с темой «Мини-конкурс № 4: любимая геометрия» и не забывайте про доказательство.

ps. Не забывайте читать комментарии, возможно будут подсказки и/или ход событий.

pss. Хотите первые узнавать о новых конкурсах? Подписывайтесь на rss :

Поделитесь с друзьями:
Tags:
Как-то странно отключилась

Как-то странно отключилась возможность комментариев, исправил.

Пока поступившие ответы не являются правильными.

Вопрос-ответ:

мне вот интересно, 1 грамм золота - в каком виде разыгрывается? :)

WebMoney WMG (Gold).

Почём нынче 1 грамм золота?

24-25 wmz, если не устраивает линк в посте, зайдите на биржу обмена WM wm.exchanger.ru :)

Опубликовано GogA в Вс, 23/11/2008 - 19:09.
решил, но с доказательством

решил, но с доказательством оказалось немного сложнее..

Опубликовано speloff (не проверено) в Вс, 23/11/2008 - 20:52.
Сейчас разбираюсь с вашим

Сейчас разбираюсь с вашим вариантом,
доказательство не до конца полное/точное.

Опубликовано GogA в Вс, 23/11/2008 - 21:44.
а треугольники могут

а треугольники могут накладываться, пересекаться?

Опубликовано Galeodor (не проверено) в Вс, 23/11/2008 - 21:28.
Считай что у тебя есть ткань,

Считай что у тебя есть ткань, в виде данной фигуры. И её надо разрезать на равнобедренные треугольники.

Опубликовано GogA в Вс, 23/11/2008 - 21:43.
Борюс с треугольниками :)

Послал уже второй солюшн, мой первый был разбит в пух и прах.

Опубликовано Jman (не проверено) в Вс, 23/11/2008 - 22:51.
Всё, я стопудов решил

В письме есть картинка, а вследующем - подробное доказательство. Если не секрет, откуда задачка?

Опубликовано Jman (не проверено) в Пнд, 24/11/2008 - 00:12.
Заглянул сейчас на почту,

Заглянул сейчас на почту, увидел два решения.
От speloff (22:32) и Jman (23:10).

Что удивительно, между собой решения очень похожи. Даже в доказательстве упущены одинаковые факты (незначительные).

Тем не менее в решении speloff были рассмотрены частные случаи данной фигуры, и ответ пришёл раньше.

speloff, поздравляю!

Jman, у вас почти правильное решение, на почту указание недочётов.
Участвуйте ещё :)

Опубликовано GogA в Пнд, 24/11/2008 - 01:34.
хех )))

ты что, думаешь, я в воскресенье не читал условия? читал)))

приехал я как дурак в офис в воскресенье... а тут...

опаньки... потом подумал-подумал... неееееееееееее, Александр, в выходной ты мой мозг не убьеш... и домой поехал )))

Опубликовано NePo (не проверено) в Пнд, 24/11/2008 - 08:52.
Будни настали, теперь можно

Будни настали, теперь можно захвать мозг?

А так порешай, интересная задачка :)

Опубликовано GogA в Пнд, 24/11/2008 - 09:08.
не-не-не-не...

... я лушче поработаю -_-

Опубликовано NePo (не проверено) в Пнд, 24/11/2008 - 09:11.
Эта задачка оказалась совсем

Эта задачка оказалась совсем простая :)

Доказал вчера буквально в три строчки что любой четырёхугольник (4 точки на плоскости, любые три из которых не лежат на одной прямой) можно всегда разделить на число равнобедренных треугольников больших или равных 8.

Желающим предлагаю поломать голову :)

Опубликовано GogA в Втр, 25/11/2008 - 10:45.
Ну, на 8 треугольников - это

Ну, на 8 треугольников - это просто. А вот на 9 чего-то не придумывается. Можно какую-нибудь подсказку, плз?

Опубликовано Stervolya (не проверено) в Сб, 06/12/2008 - 00:47.
Есть минимум два способа

Есть минимум два способа решения этой задачи.

Один не требует дополнительных знаний геометрии, даже сложных теорем знать не надо. Так что попытайтесь найти простое решение.

Опубликовано GogA в Сб, 06/12/2008 - 11:35.
А-а-а-а!

Расскажи, пожалуйста!!!

Опубликовано Igorrok (не проверено) в Вс, 14/12/2008 - 00:36.

Отправить комментарий

Содержимое этого поля является приватным и не будет отображаться публично.
  • Адреса страниц и электронной почты автоматически преобразуются в ссылки.
  • Доступные HTML теги: <em> <strong> <cite> <code> <ul> <ol> <li> <dl> <dt> <dd> <blockquote>
  • Строки и параграфы переносятся автоматически.

Подробнее о форматировании

КАПЧА
Этот вопрос задается для того, чтобы выяснить, являетесь ли Вы человеком или представляете из себя автоматическую спам-рассылку.
      _     _          _   ____       _    
   __| |   (_) __  __ (_) / ___|     / \   
  / _` |   | | \ \/ / | | \___ \    / _ \  
 | (_| |   | |  >  <  | |  ___) |  / ___ \ 
  \__,_|  _/ | /_/\_\ |_| |____/  /_/   \_\
         |__/
Введите код, изображенный в стиле ASCII-арт.

Подпишись

Подпишись на RSS!

Друзья сайта

Последние комментарии

Регистрация доменов ru